一次函數的定義是什么?一次函數的性質
時間:2023-06-24 10:04:38來源:考試幫手網作者:小黃鴨
今天小編要給大家介紹的是一次函數,一次函數的定義是什么?一次函數的性質和圖像是什么?下面跟著小編一起來看看吧!

一次函數是函數中的一種,一般形如y=kx+b(k,b是常數,k≠0),其中x是自變量,y是因變量。特別地,當b=0時,y=kx(k為常數,k≠0),y叫做x的正比例函數。
一次函數及其圖象是初中代數的重要內容,也是高中解析幾何的基石,更是中考的重點考查內容。
一次函數有三種表示方法,如下:
1、解析式法
用含自變量x的式子表示函數的方法叫做解析式法。
2、列表法
把一系列x的值對應的函數值y列成一個表來表示的函數關系的方法叫做列表法。
3、圖像法
用圖象來表示函數關系的方法叫做圖象法。
一次函數的解析式為:
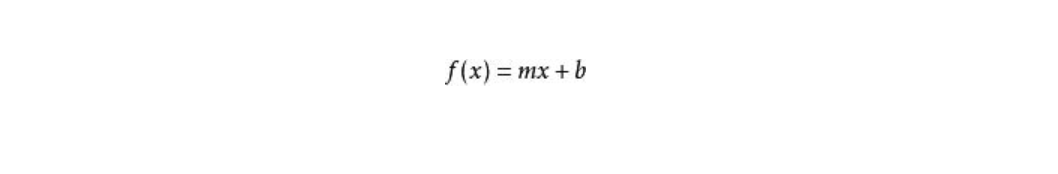
其中m是斜率,不能為0;x表示自變量,b表示y軸截距。且m和b均為常數。先設出函數解析式,再根據條件確定解析式中未知的斜率,從而得出解析式。該解析式類似于直線方程中的斜截式。
下面來看看一次函數的性質:
1、y的變化值與對應的x的變化值成正比例,比值為k。
即:y=kx+b(k≠0)(k不等于0,且k,b為常數)。
2、當x=0時,b為函數在y軸上的交點,坐標為(0,b)。
當y=0時,該函數圖象在x軸上的交點坐標為(-b/k,0)。
3、k為一次函數y=kx+b的斜率,k=tanθ(角θ為一次函數圖象與x軸正方向夾角,θ≠90°)。
4、當b=0時(即y=kx),一次函數圖象變為正比例函數,正比例函數是特殊的一次函數。
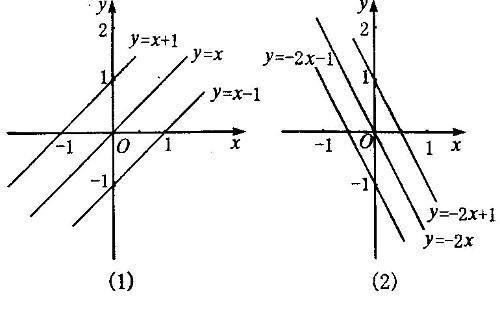
5、函數圖象性質:當k相同,且b不相等,圖像平行;
當k不同,且b相等,圖象相交于Y軸;
當k互為負倒數時,兩直線垂直。
6、平移時:上加下減在末尾,左加右減在中間。

一次函數是函數中的一種,一般形如y=kx+b(k,b是常數,k≠0),其中x是自變量,y是因變量。特別地,當b=0時,y=kx(k為常數,k≠0),y叫做x的正比例函數。
一次函數及其圖象是初中代數的重要內容,也是高中解析幾何的基石,更是中考的重點考查內容。
一次函數有三種表示方法,如下:
1、解析式法
用含自變量x的式子表示函數的方法叫做解析式法。
2、列表法
把一系列x的值對應的函數值y列成一個表來表示的函數關系的方法叫做列表法。
3、圖像法
用圖象來表示函數關系的方法叫做圖象法。

一次函數的解析式為:
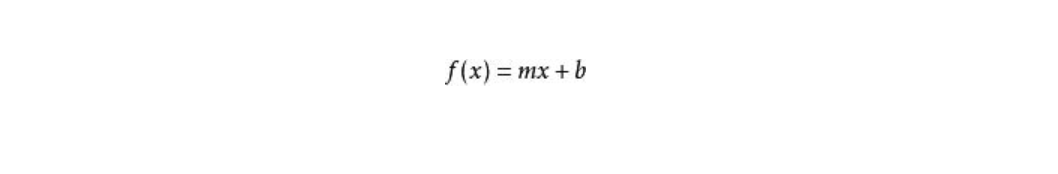
其中m是斜率,不能為0;x表示自變量,b表示y軸截距。且m和b均為常數。先設出函數解析式,再根據條件確定解析式中未知的斜率,從而得出解析式。該解析式類似于直線方程中的斜截式。
下面來看看一次函數的性質:
1、y的變化值與對應的x的變化值成正比例,比值為k。
即:y=kx+b(k≠0)(k不等于0,且k,b為常數)。
2、當x=0時,b為函數在y軸上的交點,坐標為(0,b)。
當y=0時,該函數圖象在x軸上的交點坐標為(-b/k,0)。
3、k為一次函數y=kx+b的斜率,k=tanθ(角θ為一次函數圖象與x軸正方向夾角,θ≠90°)。
4、當b=0時(即y=kx),一次函數圖象變為正比例函數,正比例函數是特殊的一次函數。
5、函數圖象性質:當k相同,且b不相等,圖像平行;
當k不同,且b相等,圖象相交于Y軸;
當k互為負倒數時,兩直線垂直。
6、平移時:上加下減在末尾,左加右減在中間。
相關推薦

-
梯形面積公式和周長公式 梯形的定義
梯形是多邊形和四邊形的一種,關于梯形的判定、面積公式、周長公式等等是數學中常見的知識點,也是必考的知

-
特殊角的三角函數值,完整初中三角函數值表
三角函數不僅是初中學習的知識點,也是高中學習的重要知識點。三角函數學習的好不好關鍵在于三角函數的公式

-
二次函數的圖像和性質?二次函數中考壓軸題
二次函數是初中數學中非常重要的一個知識點,2020年中考馬上就要到了,不知道大家對于二次函數的知識點有沒